Q: Pendulum Motion of Text book (In class 2/22 conceptual question). After you explained this question in class I was still confused. How can the book accelerate to the right at the bottom, if the only forces acting on it are pushing it up and down? Trying to rationalize this answer, is this because it is at the bottom, the book is switching from accelerating to derating so it still has the velocity to the right, but know forces pushing it left or right?
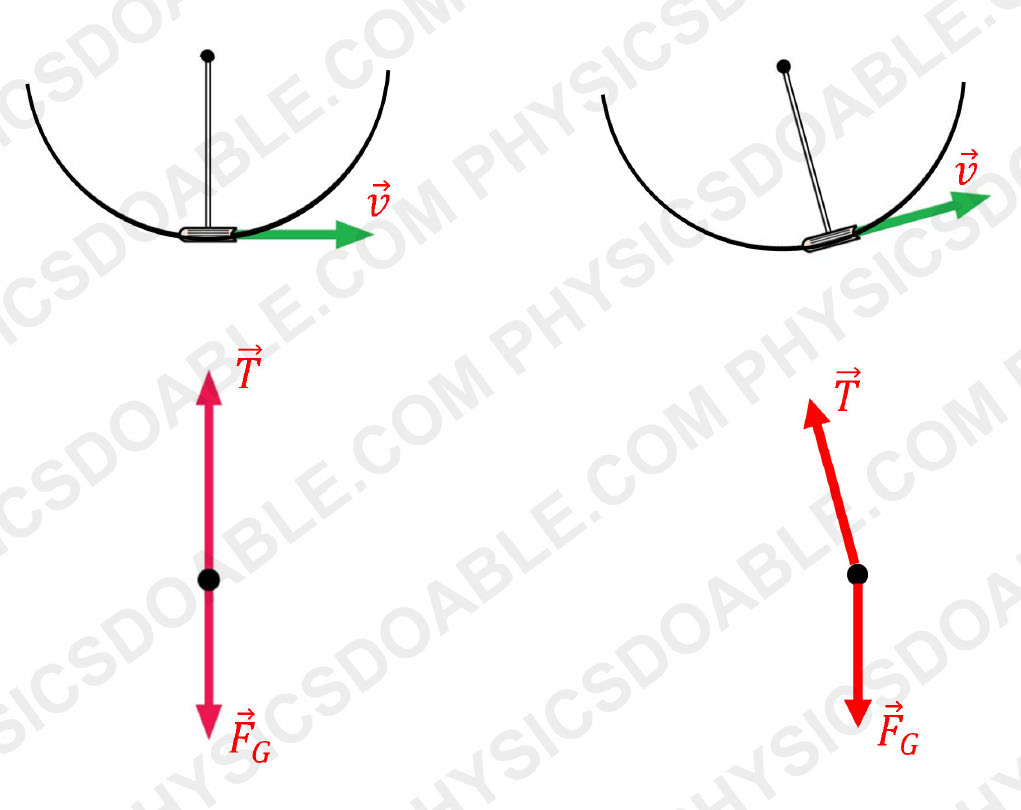
A: The free body diagram shown in lecture (also on the LEFT in the picture here) is ONLY for this position/instant (bottom). At this bottom position, the net force in Radial direction (also called “Centripetal Force”) is upward since the center of the circle is above the object, while the net force in Tangential direction is zero. However, the tangential velocity is to the right at this instant.
When the object moves away from the bottom position, just a little to the right, the situation of forces will be very different. The free body diagram for this case is given on the RIGHT in the picture here. The the net force in Radial direction (also called “Centripetal Force”) is still pointing to the center of the circle, while the net force in Tangential direction is non-zero, which comes from a component of Gravity/Weight. Yes, you reasoning is correct here: it is de-accelerating/slowing-down!
In addition, the Pendulum topic will be further discussed in Physics 132 course.
Q: For a car moving on banked curves, does static friction come up acting opposite to the normal force in the r direction? Also, I was having trouble understanding when and when not to use static friction.
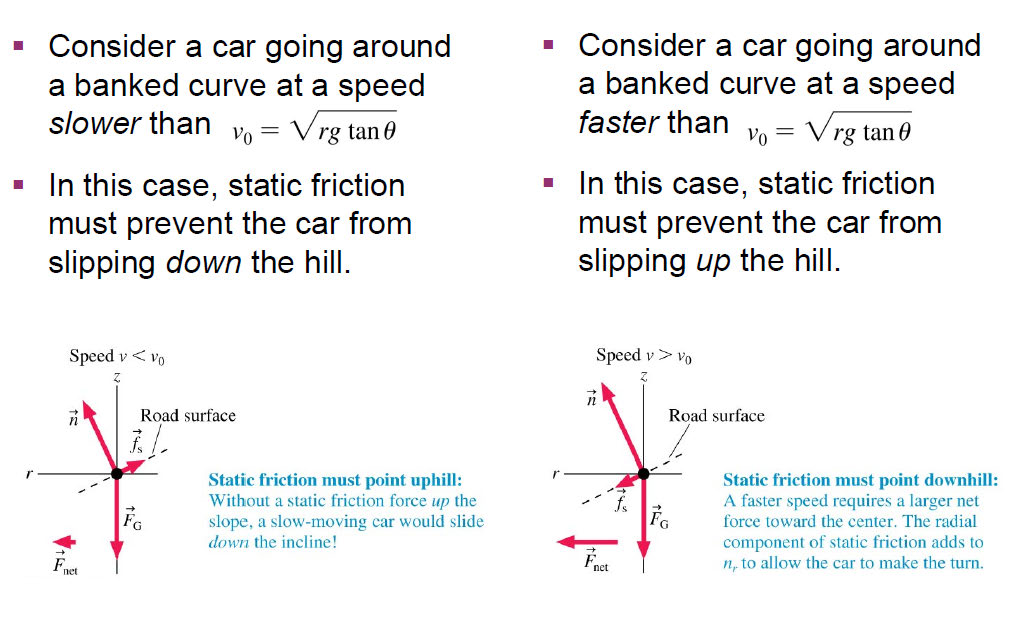
A: It depends on the speed/tangential velocity. First we need to find the critical speed at which the centripetal force is provided by the normal force alone. In other words, static friction equals to zero at this speed.
- If the speed is then lower than the critical value, static friction contributes negatively to centripetal force. In other words, static friction and normal force have radial components opposite in direction.
- If the speed is then higher than the critical value, static friction contributes positively to centripetal force. In other words, static friction and normal force have radial components parallel in direction.
In simple words, if normal force alone is not good enough to provide Centripetal force in Radial direction and balances with Gravity in Z direction. We need to have Static friction involved. Refer to the picture attached.
